- (a) Three events A, B and C are mutually exclusive events and their probabilities are P (A) = 2/3, P (B) = 1/2 and P (C) = 1/6. Comment on the result.
Solution:
Given that events A, B, and C are mutually exclusive, it means that no two events can occur simultaneously. In other words, the occurrence of one event excludes the occurrence of the other events.
The probabilities given are:
P(A) = 2/3
P(B) = 1/2
P(C) = 1/6
For mutually exclusive events, the probability of the union of the events (i.e., the probability that at least one of them occurs) is the sum of their individual probabilities:
P(A∪B∪C)=P(A)+P(B)+P(C)
Now,
P (AUBUC) = (2/3) + (1/2) + (1/6)
Firstly, we need to find the common denominator:
2/3 = (2*2) / (3*2) = 4/6
1/2 = (1*3) / (2*3) = 3/6
1/6 = remains same as the denominator is already 6
Adding these all,
(AUBUC) = (4/6) +(3/6) + (1/6)
= 4/3
Here, the result (4/3) is greater than 1, which is impossible since the probability of any event or combination of events cannot exceed 1.
Answer: Inconsistent
(b) The probabilities of increasing and decreasing of price of a commodity are 0.35 and 0.55 respectively. What is the probability of remains constant the price of the commodity?
Solution:
To determine the probability that the price of the commodity remains constant, you can use the fact that the sum of all possible outcomes must equal 1 (since probabilities always add up to 1).
Let,
P (Increase) = 0.35
P (Decrease) = 0.55
P (Constant) be the constant price.
Since the price can only increase, decrease, or remain constant, we have:
P(Increase)+P(Decrease)+P(Constant)=1
or, 0.35 + 0.55 + P (Constant) = 1
or, P (Constant) = 1 – 0.35 + 0.55
or, P (Constant) = 1 – 0.90
Hence, P (Constant) = 0.10
So, the probability that the price of the commodity remains constant is 0.10 or 10%.
- The manager of a furniture store sells from 0 to 4 ‘China hutches’ each week. On the basis of past experience, the following probabilities are assigned to sales of 0,1,2,3 or 4 hutches:
P(0) = 0.08
P (1) = 0.18
P (2) = 0.32
P (3) = 0.30
P (4) = 0.12
Questions
a. Are these valid probability assignments ? Why or Why not?
Solution
To determine if these are valid probability assignments or not, we need to check the following two conditions:
First condition: Non-negativity: Each probability must be between 0 and 1, inclusive.
Second Condition: Total Probability: The sum of all probabilities must equal 1
Checking first Condition:
Each probability value is within the range [0, 1]:
The probability of P(0) = 0.08 is within the range of 0 to 1.
The probability of P (1) = 0.18 is within the range of 0 to 1.
The probability of P (2) = 0.32 is within the range of 0 to 1.
The probability of P (3) = 0.30 is within the range of 0 to 1.
The probability of P (4) = 0.12 is within the range of 0 to 1.
Hence, from first condition its valid.
Checking second Condition:
The sum of all probabilities should equal 1:
= P(0) + P(1) + P(2) + P(3) + P(4)
= 0.08+0.18+0.32+0.30+0.12
= 1
Since the total sum equals 1, the second condition is also satisfied.
Conclusion: Yes, these are valid probability assignments because they meet both conditions: all probabilities are non-negative and their total sum equals 1.
b. Let A be the event that 2 or fewer are sold in one week. find P (A).
Solution
Event A includes the cases where the number of hutches sold is 0, 1, or 2. So, the probability of A is:
P(A)=P(0)+P(1)+P(2)
= 0.08 + 0.18 + 0.32
= 0.58
Thus, the probability that 2 or fewer hutches are sold in one week, is 0.58 or 58 %
c. Let B be the event that 4 or more are sold in one week. Find P(B).
Solution
Event B includes the cases where the number of hutches sold is 4 or more. So, the probability of B is:
P (B) = P (4)
= 0.12
Thus, the probability that 2 or fewer hutches are sold in one week, is 0.12 or 12 %
- A survey of 50 students at a certain college about the number of extracurricular activities resulted in the data shown.
| Number of activities | Frequency |
|---|---|
| 0 1 2 3 4 5 | 8 20 12 6 3 1 |
a. Let A be the event that a student participates in at least 1 activity. Find P (A).
Solution
The probability P(A) is the ratio of the number of students participating in at least 1 activity to the total number of students:
P (A) = Number of students in A / Total number of students
= (20+12+6+3+1) / 50
= 42 / 50
= 0.84
The probability that a student participates in at least 1 extracurricular activity, P (A) is 0.84 or 84 %.
b. Let B be the event that a student participates in 3 or more activities. Find P (B).
Solution
The probability P(B) is the ratio of the number of students participating in at least 3 activity to the total number of students:
P (B) = Number of students in B / Total number of students
= (6+3+1) / 50
= 10 / 50
= 0.2
The probability that a student participates in at least 3 or more extracurricular activity, P (B) is 0.12 or 20%.
c. What is the probability that a student participates in exactly 2 activities?
Solution:
Let P(C) be the number a student that participates in exactly 2 activities.
The probability P(C) is the ratio of the number of students participating in exact 2 activity to the total number of students:
P (C) = Number of students in C / Total number of students
= 12 / 50
= 0.24
Hence, the probability that a student participates in exactly 2 extracurricular activity, P (C) is 0.24or 24%.
d. What is the probability that a student participates at most 2 activities?
Solution
Let P(D) be the number a student that participates in at most 2 activities.
The probability P(D) is the ratio of the number of students participating in at most 2 activity to the total number of students:
P (D) = Number of students in D / Total number of students
= (8 + 20 + 12) /50
= 0.8
Hence, the probability that a student participates in at most 2 extracurricular activity, P (D) is 0.8 or 80%.
- What is the chance that a non-leap year should have fifty-three Sundays?
Solution:
Remember,
- A non-leap year has 365 days.
- 365 days can be divided into 52 weeks and 1 extra day (since 365÷7=52 with a remainder of 1).
Step 2: Determine the Extra Day
The extra day could be any day of the week: Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, or Saturday.
Step 3: Favorable Outcomes
For a non-leap year to have 53 Sundays, the extra day must be a Sunday.
Step 4: Total Possible Outcomes
There are 7 possible outcomes for the extra day (one for each day of the week).
Step 5: Probability Calculation
Since the extra day could be a Sunday with a probability of 1 out of 7:
P (53 Sundays) = 1/7
The probability that a non-leap year has 53 Sundays is 1/7 which is approx. 0.1429 or 14.29 %
- If two coins are tossed once, what is the probability of getting (a)both heads (b) at least head
Solution:
When two coins are tossed, each coin has two possible outcomes: heads (H) or tails (T). The possible outcomes for two coins are:
- HH (both heads)
- HT (one head, one tail)
- TH (one tail, one head)
- TT (both tails)
So, there are 4 possible outcomes in total.
Presenting it in table:
| Coin 1 | Coin 2 | Outcome |
|---|---|---|
| H H T T | H T H T | HH HT TH TT |
(a)both heads
To find the probability of getting both heads (HH):
- Favorable outcome: HH
- Total possible outcomes: 4 (HH, HT, TH, TT)
P(Both Heads) = Number of favorable outcomes / Total possible outcomes
= 1 /4
The probability of getting at least one head when two coins are tossed is 1/4 or 25%.
(b) at least head
The event “at least one head” occurs if any of the following outcomes happen:
- HH
- HT
- TH
There are 3 favorable outcomes where at least one head appears.
P(at least one Head) = Number of favorable outcomes / Total possible outcomes
= 3 / 4
The probability of getting at least one head when two coins are tossed is 3/4 or 75%.
- In a single throw of two dice, find the probability that the sum of two faces is (a) 8, (b) 5 or 7, (c) 7 or 11.
Here,
n= Exhaustive number of outcomes in throwing two dice = 6 * 6 = 36
The sample space (total outcomes) are presented below:
a. Solution
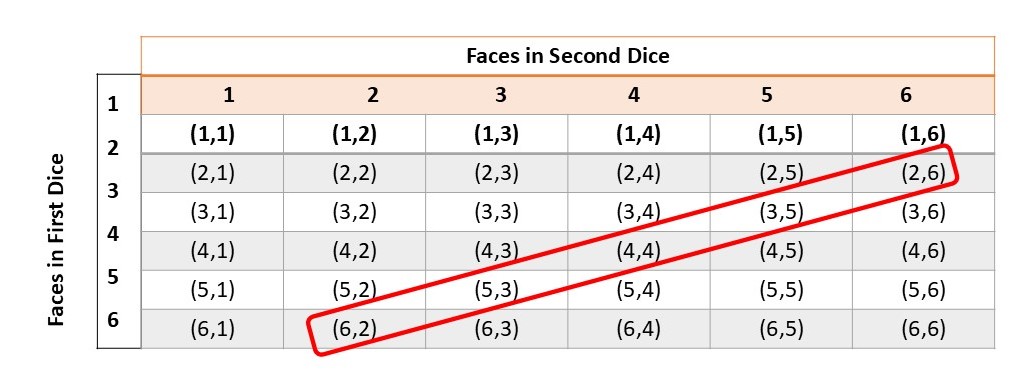
P(8) = Total Favorable events / Total exhaustive events
= [(6,2) (5,3) (4,4) (3,5) (2,6)] / 36
= 5 / 36
b. Solution
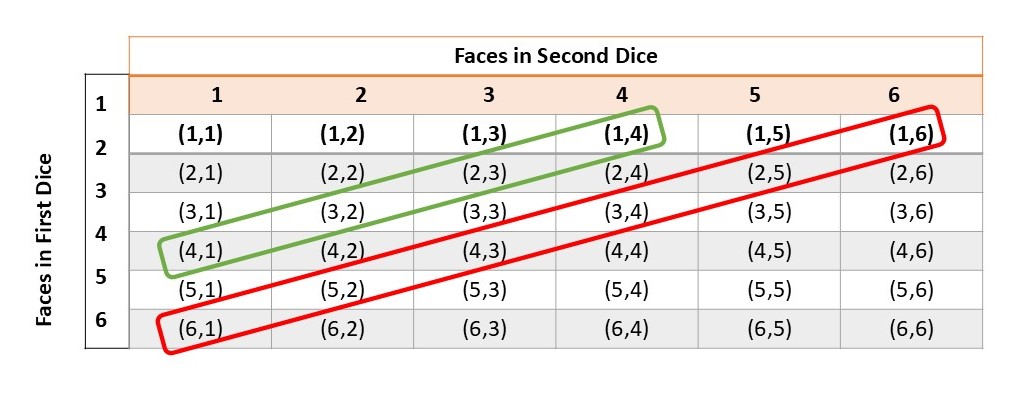
Favorable number of outcomes
= getting a sum 5 or 7
= (4,1) (3,2) (2,3) (1,4) (6,1) (5,2) (4,3) (3,4) (2,5) (1,6)
m = 10
P (Sum is 5 or 7) = 10/36 =5/18
c. Solution
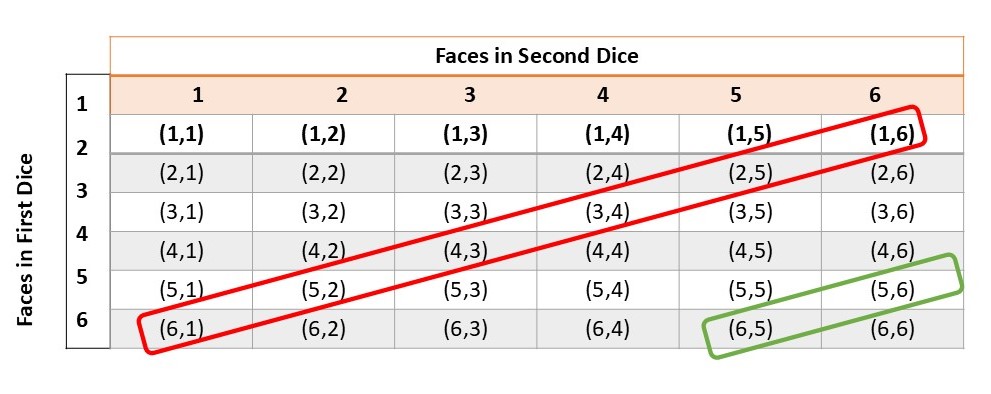
Favorable number of outcomes
= getting a sum 7 or 11
= (6,5) (5,6) (6,1) (5,2) (4,3) (3,4) (2,5) (1,6)
m = 8
P (Sum is 7 or 11) = 8/36 =2/9
- If an unbiased coin is flipper thrice, find the probability of getting (a) all three heads (b) at least one head (c) four tails.
Solution
When an unbiased coin is flipped three times, each flip can result in either heads (H) or tails (T). This gives us
Exhaustive Cases = n
= 23
= 8 possible outcomes
Presenting it in table for understanding:
| First Flip | Second Flip | Third Flip | Outcome |
|---|---|---|---|
| H H H H T T T T | H H T T T T H H | H T T H T H H T | HHH HHT HTT HTH TTT TTH THH THT |
| Just for understanding in more easier way |
|---|
| If you flipped a coin one time then you have probabilities of getting: (HH) (HT) (TT) (TH) So if you multiply these all by H and T again then you would get the probabilities coin three times then you would get: Firstly multiply by H : = H(HH) H(HT) H(TT) H(TH) = (HHH) (HHT) (HTT) (HTH) Secondly multiply by T : = T(HH) T(HT) T(TT) T(TH) = (THH) (THT) (TTT) (TTH) So while adding both the final result is: = (HHH) (HHT) (HTT) (HTH) (THH) (THT) (TTT) (TTH) |
(a) all three heads
Solution
The favorable outcome for getting all three heads is HHH.
Number of favorable outcomes (m)= HHH
Total possible outcomes (n)= 8
The probability of getting all three heads P(all three heads) = m/n
= 1/8
(b) at least one head
Solution
The event “at least one head” means getting one or more heads in the three flips. The only outcome that does not include a head is ‘TTT’.
Number of favorable outcomes (m): 7 (all outcomes except TTT)
Total possible outcomes (n): 8
The probability of getting all three heads P(all three heads) = m/n
= 7 / 8
(c) four tails.
Solution
Since the coin is only flipped three times, it is impossible to get four tails. Therefore:
P (four tails) = 0
- A bag contains 20 tickets marked with number 1 to 20. One ticket is drawn at random. Find the probability that will be multiple of
(a) 2 or 5 (b) 3 or 5 (c) 4 or 7 (d) 2 and 5
(a) 2 or 5
Solution
Out of 20 tickets 1 can be drawn as 20c1 ways
i.e. exhaustive number n = 20
Let, P(A) be the multiples of 2 and
P(B) be the multiples of 5
The numbers which are multiple of 2 = P(A)
={2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
= 10/20
= 1/2
and
The numbers which are multiple of 5 = P (B)
= {5, 10, 15, 20}
= 4/ 20
= 1/5
Common for both (A∩B)
= {10, 20}
= 2/20
= 1/10
P(AUB) = P(A) + P(B) – P (A∩B)
= (1/2) + (1/5) – (1/10)
= 3/5
Hence, the probability that the number drawn is a multiple of 2 or 5 is 3/5 or 60%.
| You can also solve this simply by this way |
|---|
| number of favorable cases for 2, 5 = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20} and {5, 10, 15, 20} common for both = {10, 20} m = 14-2 = 12 Required probability for multiple of 2 or 5 = m/n = 12/20 = 3/5 = 0.6 = 60% |
(b) 3 or 5
Solution
Let P(A) be the multiple of 3 and
P(B) be the multiple of 5
The numbers which are multiple of 3 = P(A)= {3, 6, 9, 12, 15, 18}
= 6 / 20
= 3/10
The numbers which are multiple of 5 = P (B)
= {5, 10, 15, 20}
= 4/ 20
= 1/5
Common for both (A∩B)
= {15}
= 1/20
P(AUB) = P(A) + P(B) – P (A∩B)
= (3/10) + (1/5) – (1/20)
= 9 /20
=0.45
= 45%
Hence, the probability that the number drawn is a multiple of 3 or 5 is 9/20 or 45%.
(c) 4 or 7
Solution
Let P(A) be the multiple of 4 and
P(B) be the multiple of 7
The numbers which are multiple of 4 = P(A)
= {4, 8, 12, 16, 20}
= 5/ 20
= 1/4
The numbers which are multiple of 7 = P(B)
= {7, 14}
= 2 /20
= 1 /10
Common for both (A∩B)
= 0
P(AUB) = P(A) + P(B) – P (A∩B)
= (1/4) + (1/10) – 0
= 7/20
= 0.35
= 35 %
Hence, the probability that the number drawn is a multiple of 4 or 7 is 0.35 or 35%.
(d) 2 and 5
Solution
Let P(A) be the multiple of 2 and
P(B) be the multiple of 5
The numbers which are multiple of 2 = P(A)
={2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
= 10/20
= 1/2
and
The numbers which are multiple of 5 = P (B)
= {5, 10, 15, 20}
= 4/ 20
= 1/5
Common for both (A∩B)
= {10, 20}
= 2/20
= 1/10
P(A and B) = P(A) * P(B)
= (1/2) * (1/5)
= 1/10
= 0.1
= 10%
Hence, the probability that the number drawn is a multiple of 2 and 5 is 1/10 or 10%.
- A card is drawn from a well shuffled pack of playing cards. Find the probability that it is (a) either a diamond or a king (b) black or queen.
There are 52 cards in a pack which is the sample space or exhaustive events
i.e. n = Total number of outcomes = 52
(a) either a diamond or a king
Solution
Let A denotes the event of drawing either a diamond or a king cards, then favorable number of outcomes = Drawing diamond cards or king
= 13 + 4 -1
=16
Required probability
P ( Either Diamonds or Kings) = P(A)
= Favorable number of outcomes / Total number of outcomes
P(A) = m/n
= 16 / 52
=4/13
(b) black or queen
Solution
Let B denotes the event of drawing black or queen cards, then favorable number of outcomes = Drawing black cards or queen
= (13 + 13) + 4 – 2
= 28
P ( Black or queen) = P(B)
= Favorable number of outcomes / Total number of outcomes
P(B) = m/n
= 28/ 52
=7/13
- A survey of magazine subscriber showed that 45.8% rented a car during the past 12 months for business reasons, 54 % rented a car during the past 12 months for personal reasons, and 30 % rented a car during the past 12 months for both business and personal reasons.
Solution
Let P(A) represent the magazine subscriber who rented car for business reasons
P(B) represent the magazine subscriber who rented car for personal reasons
P(A∩B) represent the magazine subscriber who rented car for both reasons
Then,
P(A) = 45.8% = 45.8/100 =0.458
P (B) = 54 % = 54/100 =0.54
P(A∩B) = 30 % = 30/100 = 0.30
a. What is the probability that a subscriber rented a car during the past 12 months for business or personal reasons?
Solution
P(AUB) = P(A) + P(B) – P (A∩B)
= 0.458 + 0.54 – 0.30
= 0.698
= 69.8%
b. What is the probability that a subscriber did not rent a car during the past 12 months for either business or personal reasons?
Solution
We already know that,
P(AUB) = 0.698
Using complement rule,
P(Not(AUB)) = 1 – P(AUB)
= 1 – 0.698
= 0.302
Hence, the probability that a subscriber did not rent a car during the past 12 months for either business or personal reasons is 0.302 or 30.2%.
- Mr. A and Mr. B both are interested to attend a seminar in Central Department of Statistics, TU. The chance of attending a seminar by Mr. A is 0.6 and that by Mr. B is 0.3. They both can also attend the seminar. What is the probability that at least any one of them will attend the seminar?
Solution
Let P(A) represent Mr.A and
P(B) represent Mr.B
Given information are:
P(A) = 0.6
P(B) = 0.3
P(A∩B) = Not given
Let us first calculate P(A∩B)
P(A∩B)= P(A) * P(B)
= 0.6 * 0.3
= 0.18
Now, Probability that at least any one of them will attend the seminar =
P(A or B) = P(A) + P(B) – P(A∩B)
= 0.6 + 0.3 – 0.18
= 0.72
Hence, the probability that at least any one of them will attend the seminar is 0.72 or 72%.
- The probability that a student passes in economics test is 3/4 and the probability that he passes both economics and management test is 12/40. The probability that he passes at least one test is 5/6. Find the probability that he will pass in the management test.
Solution
Let P(E) represent students passes in economics test, and
P(M) represent students passes in management test, and
P(E∩M) represent students passes in both economic and management, and
P(EUM) represent students that passes at least one test
Given information are:
P(E) = 3/4 represents the probability that the student passes the economics test.
P(E∩M) = 12/40 = 3/10 represents the probability that the student passes both the economics and management tests.
P(EUM) = 5/6 represents the probability that the student passes at least one of the tests either economics or management or both
Now,
We need to find the probability that the student passes the management test, P(B)
P(E∪M) = P(E) + P(M) – P(E∩M)
(5/6) = (3/4) + P(M) – (3/10)
P(M) = (5/6) – (3/4) + (3/10)
P(M) = 23/60
Hence, the probability that the student will pass the management test is 23/60 or approximately 0.3833 or 38.33%
- The probability that an integrated circuit chip will have defecting etching is 0.12, the probability that it will have a crack defect is 0.29, and the probability that it has both defects is 0.07.
Let P (E) represent the integrated circuit chip that will have defecting etching, and
P (C) represent the integrated circuit chip that will have crack defect
P(E∩C) represent the integrated circuit chip that will have both defects
Given information are:
P(E) = 0.12
P(C) = 0.29
P(E∩C) = 0.07
a. What is the probability that a newly manufactured chip will have at least one of two defects?
Solution
P(E or C) = P(E) + P(C) – P(E∩C)
= 0.12 + 0.29 – 0.07
= 0.34
Hence, the probability that a newly manufactured chip will have at least one of two defects is 0.34 or 34%
b. What is the probability that a newly manufactured chip will have neither any kind of two defects?
Solution
P(Not (EUC)) = 1 – P(EUC)
= 1 – 0.34
= 0.66
= 66%
- The odds are 9 to 5 against a person who is 50 years living till he is 70 and 8 to 6 against a person who is 60 living till he is 80. Find the probability that at least one of them will be alive after 20 years.
Solution
Given,
Probability that person lives till he is 70 = P(A) = [9/(9+5)] = 9/14
Probability that person doesn’t lives till he is 70 = P(Ac) = [5/(9+5)] = 5/14
or you can also calculate this by:
= 1 – (9/14)
= 5/14
and,
Probability that person lives till he is 60= P(B) = [8/(8+6)] =4/7
Probability that person doesn’t lives till he is 60= P(Bc)
= 1 – P(B)
= 1 – (4/7)
= 3/7
The probability that at least one of them will be alive after 20 years is the complement of the probability that both will not be alive. We use the following formula:
P(At least one survives) = 1 − P(Both do not survive)
where,
P(Both do not survive)=P(50-year-old does not survive)×P(60-year-old does not survive)
Substituting the value,
P(Both do not survive)= 9/14 * 4/7
=36/98
= 18/49
Now, let’s calculate the probability that at least one survives:
P(At least one survives)=1− (18/49)
=31/49
The probability that at least one of them will be alive after 20 years is 31/49 or approximately 0.6327 or 63.27%
- The salesman has a 60% chance of making a sale to each customer. The behavior of successive customers is independent. If two customer A and B enter, what is probability that the salesman will make a sale to A or B?
Solution
- A person is known to hit the target in 3 out of 4 shots, whereas another person is known to hit the target in 2 out of 3 shots. Find the probability of the targets being hit at all when they both try?
Solution
- The probability that the man will be alive 25 years is 3/5 and the probability that his wife will be alive 25 years is 2/3.
Find the probability that
a. both will be alive
b. only the man will be alive
c. only the wife will be alive
d. at least one will be alive
e. none will be alive, 25 years hence
f. only one of them will be alive 25 years hence.
Solution
- A bag contains 7 red, 12 white and 4 green balls. Three balls are drawn randomly. What is the probability that
a. 3 balls are all white and
b. 3 balls are one of each color.
Solution
- (a) A bag contains 7 white and 9 black balls. Two balls are drawn in succession at random with replacement. What is the probability that one of them is white and other is black?
Solution
(b) A bag contains 3 red, 4 white and 5 black balls. three balls are drawn from the bag. Find the probability that:
(i) all are black (ii) all are of different colour
Solution
- There are 3 economists, 4 engineers, 2 statisticians and 1 doctor. A committee of 4 from them is being formed. Find the probability that the committee
a. consists one of each kind
b. has at least one economist
c. has the doctor as a men and three others.
Solution
